Investigation of cathode spot behaviour of atmospheric argon arcs by mathematical modelling
J. Wendelstorf 1, G. Simon2, I. Decker1 and H.Wohlfahrt1
1
Institut für Schweißtechnik and 2Institut für Theoretische Physik,Technische Universität Braunschweig
Postfach 3329, D-38023 Braunschweig, Germany
Tel.: +49.531.391-7821, Fax: +49.531.391-5834
e-mail: j.wendelstorf@tu-bs.de
ABSTRACT
The nature and behaviour of high pressure electric arcs significantly depends on the formation of the cathodic hot spot. By a quantitative comparison of modelling results with arc temperature measurements, an attempt is made towards getting information on cathodic current densities and temperatures by varying the boundary conditions of the arc column model. The values resulting in best agreement with measurement may be regarded as cathode spot parameters determined indirectly. Recent investigations towards a self-consistent computation of the stationary arc spot are also discussed.
1 INTRODUCTION
The state-of-the-art in modelling of stationary electric arcs was reviewed recently [1]. A mathematical description of the arc is based on the assumption of local thermodynamic equilibrium (LTE) within the visible part of the arc, the column [12]. This arc column, and thus the behaviour of electric arcs burning in inert gases at medium and high pressures depend strongly on the formation of the cathode spot. The physical mechanisms of cathode spot formation for the case of diffuse arc attachment to a refractory material cathode are thought as follows:
The formation of the magneto-hydrodynamic cathodic jet can be studied by solving the partial differential equations governing the arc column. Modelling of the non equilibrium effects described above is not the objective of this paper. Because integrated and self-consistent models of the overall arc discharge are extremely complex, an attempt is made to derive important cathode spot parameters like the peak current density from a comparison of measured and computed arc temperatures.
2 ARC MEASUREMENTS USED
The experimental determination of arc parameters is undertaken since the onset of plasma physics itself. For the case of a DCEN-argon arc burning between a copper anode and a (thoriated) tungsten cathode, a remarkable amount of experimental data was published in open literature.
Following the experiments of Olsen [2] and Nestor [3], the split anode determination of the anodic arc current density distribution is now available for a number of arc configurations [4]. The excess pressure distribution at the anode surface was determined in a similar manner [5]. Additionally, the split anode approach can be extended to deal with non radial symmetric arcs [6].
The experimental data and arc configurations used for this work was taken from the spectroscopic arc temperature determinations published by the group of Pfender [7], at the CSRIO in Australia [8-12] and by Thornton [13].
3 THE ARC MODEL
The mathematical model of the arc column is described in detail in the recent review [1]. It is two-dimensional, assuming a stationary arc with radial symmetry. Thus arc temperature T, static pressure p and fluid velocity v are computed in dependence of the radial and axial space co-ordinates r and z (see figure 1). Full account is taken for the temperature dependence of the transport coefficients and the equations are solved by a finite difference method on a non equidistant numerical grid. The geometry used was taken from the individual publications containing the experimental arc temperature measurements described above.
Figure 1: Definition of the arc column modelling problem.
To obtain a treatable inverse problem for the boundary conditions at the cathode surface, the following assumption on the radial current density distribution was made:
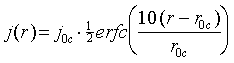 .
.
Similar distributions were used for the temperature boundary condition. In earlier papers, exponential or gaussian distributions were often used. These type of boundary conditions was found to give deviations from spectroscopic arc temperature data which are outside the measurement error. For finer numerical grid spacing, additionally numerical problems may occur (up to 300,000 grid cells were used for separating numerical from physical effects).
The anode temperature boundary condition was assumed to be gaussian:
![]() .
.
Thus, the number of independent parameters for the inverse problem is limited to:
|
j0c |
cathode peak current density |
|
T0c |
cathode peak plasma temperature |
|
r0a |
anode hot spot half-width |
|
T0a |
anode peak plasma temperature |
4 QUANTITATIVE COMPARISON WITH EXPERIMENTAL DATA
The spectroscopical determination of arc temperature usually comes with a measurement error of about 5-10%. Modelling accuracy depends on grid spacing and the accuracy of the plasma transport coefficients, but may be regarded as more accurate than measurement (assuming one has the exact boundary conditions).
After modelling the arc column for a given set of boundary conditions and using the arc parameters provided in the corresponding experimental papers (e.g. [7] or [13]), the relative difference between measured and computed arc temperatures given by
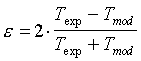 .
.
Its spatial dependence can be plotted for the individual arc configurations (see figure 2 for an example).
Figure 2: Relative deviation of measured [8] to computed arc temperatures (5mm argon arc, 0.1MPa, I=100A, j0=108 A/m2, 60° tip).
5 RESULTS
By comparison of modelling data with arc temperature measurements, no significant variation of peak current density with total arc current was observed. The major difficulty of this approach is the lack of detailed experimental data and the accuracy of arc temperature measurement: doubling the arc current (showing big differences in the application, e.g. for welding), gives a temperature map deviation of about 5-10%, which is still within the actual measurement error limits.
The arc configurations shown in table 1 were used for this study. It should be noted, there are no arc temperature determinations available, undertaken for identical arc configurations but provided by different groups (the cathode opening angles used in [13] and [8] are different).
The best fit values for the cathode boundary condition parameters can be found in table 2 for the peak current density and in table 3 for the peak plasma temperature.
|
I: larc : |
5mm |
10mm |
20mm |
|
100A |
[8, 12, 13] |
[7] |
[7] |
|
200A |
[8, 12] |
[7] |
[7] |
|
300A |
[12] |
[7] |
[7] |
Table 1: Arc temperature measurements used (for details see the references cited in the table).
|
I: larc : |
5mm |
10mm |
20mm |
|
100A |
1.0± 0.3 |
1.3± 0.2 |
1.1± 0.4 |
|
200A |
1.0± 0.4 |
1.2± 0.2 |
1.1± 0.3 |
|
300A |
1.0± 0.4 |
0.8± 0.3 |
1.0± 0.4 |
Table 2: Cathodic peak current density [108A/m2] determined from the comparison of spectroscopical arc temperature data with modelling results.
|
I: larc : |
5mm |
10mm |
20mm |
|
100A |
20.5± 1.0 |
21.0± 1.0 |
20.5± 1.0 |
|
200A |
20.5± 1.0 |
21.0± 1.0 |
21.0± 1.0 |
|
300A |
21.5± 1.0 |
21.0± 1.0 |
21.0± 1.0 |
Table 3: Cathode peak temperature [kK] determined from the comparison of spectroscopical arc temperature data with modelling results.
By showing no significant arc length dependency, the results reflect the "downstream" nature of the cathode jet (peclet number greater than 1).
Thornton measured the arc temperature distribution for a cathode with 30° included angle (tip flattened at 0.1 mm radius) [13]. Modelling this arc configuration and comparison with his data, less than 4% difference is observed. The numerical reproduceability of the other experiments (60° included angle, flattened at 0.2 mm radius) give higher differences of 5-10%. Arc models with cathodic peak current densities above 1.5 .108 A/m2 or below 0.5 .108 A/m2 differ too much from experimental data to be regarded as possible in reality. The best fit cathodic peak temperature was found to be about 5% below the maximum arc temperature derived from spectroscopy.
As a conclusion, it was found to be very difficult (or even impossible) to derive accurate cathode spot parameters by this method, while only experimental data with more than 3% measurement error is available. The dependencies of the application parameters (e.g. anodic excess pressure) are strongly influenced by these cathode parameters and thus the high accuracy is needed for obtaining applicable modelling results.
Finally, the results provide additional trust in the quality of the mathematical arc column models actually used.
6 SELF CONSISTENT ARC MODELS
During the current decade, non equilibrium effects at the electrode surfaces came into the range of mathematical modeling. First, Delalondre and Simonin included a simple sheath model into their arc column model, thus getting a mathematical description of the overall arc electrode system [16]. A similar approach was also implemented and extended by Zhu et.al. [11]. The accurate computation of the cathode fall voltage is assumed to require a sophisticated inclusion of space charge effects, the temperature split and TF-electron emission processes, which is actually under investigation [14]. Using such a detailed description of the non-equilibrium layer together with an arc column model, an attempt is made to develop a numerical model of the arc, free of internal boundaries and fitting parameters depending on the individual arc configurations.
7 CONCLUSIONS
The stationary arc discharge is governed by non-linear physical phenomena taking place in the arc column and the boundary layers. The strong interaction of these regions produce a complex self adaptive system.
Oversimplifications within the individual models of these regions or "column-only" descriptions deliver arc temperature distributions still in good agreement with spectroscopic temperature distributions. But the behaviour of the arc due to external parameter variations can not be described by this approach. The internal boundary conditions need to be determined by comparison with experimental data.
It was found to be impossible to derive the cathodic peak temperature and current density with a satisfying accuracy, without arc temperature determinations with less than 5% experimental error. The a priori prediction of application parameters (e.g. the anodic heat and pressure distribution needed for modelling of welding processes) is therefore not possible for arc configurations not investigated by experiment in advance. The actual models show very limited extrapolation capabilities.
Actually, the cathode spot formation is not computed ab initio, but derived from measurement. The results evaluate the correct description of the cathode jet formation, i.e. the mathematical model of the arc column. By inclusion of heat and current transfer in the cathode body, thermionic electron emission and modelling of the non-equilibrium plasma layer direct in front of the cathode surface, self-consistent arc models without prescribed internal boundary conditions are under development.
The range of current densities found in the hot spot of the atmospheric argon arc is 0.8 to 1.2 .108 A/m2 for total arc currents between 80 and 500A and a cathode geometry showing low erosion rates (thus forming a stable cathode shape for arcing times of more than several minutes).
8 ACKNOWLEDGEMENTS
Partial support by the german ministry for education and research (BMBF) under contract No. 13N7105/9 is greatfully acknowledged.
9 REFERENCES