In: N.N. (ed.): Proc. 8th Int. Symposium on the Science & Technology of Light Sources (LS-8), Greifswald, 30.8.-3.9.1998
Modelling of arc-electrode systems -
preliminary results for high pressure xenon arc lamps
J. Wendelstorf, I. Decker, H. Wohlfahrt and G. Simon
Technische Universität Braunschweig, Postfach 3329, D-38023 Braunschweig
http://www.ifs.ing.tu-bs.de/jw/aglbphys.html
1 Introduction
Properties like lifetime and peak intensity of high pressure arc lamps depend on the electrode plasma transition of the discharge. The main high pressure lamp plasma can be described by local thermodynamic equilibrium (LTE) models [1-3], but the formation of the cathode hot spot is not fully understood. It dominates the overall lamp system for electrode stabilised discharges (short arc lamps) and it may be responsible for the lamps lifetime (all discharges).
To compute predictions for new lamp configurations, self consistent models are required. There are two approaches currently under investigation. The model of Fischer [4] is implemented into an adaptive finite element (FEM) model by the group of Neiger [5,6] and a finite difference hydrodynamic model is extended to include non-LTE boundary layers. Initial results for the second approach are sketched in this paper.
For the validation of such models, the cathode spot transition in high pressure Xenon lamps [7] is proposed.
2 Details of the lamp model
The 2- or 3-D modelling of stationary high pressure arc columns is state-of-the-art for a number of application areas. For a 4 MPa Xe short arc lamp, Palacin [3] computed the flow field and temperature distribution in the lamp plasma and found reasonable agreement with experimental data. But pure LTE-models need boundary conditions, especially at the cathode surface. As discussed in [9], the inverse problem of deriving these boundary conditions from comparison with spectroscopic plasma temperature data will require very high experimental accuracy and the results will depend on arc configuration and current.
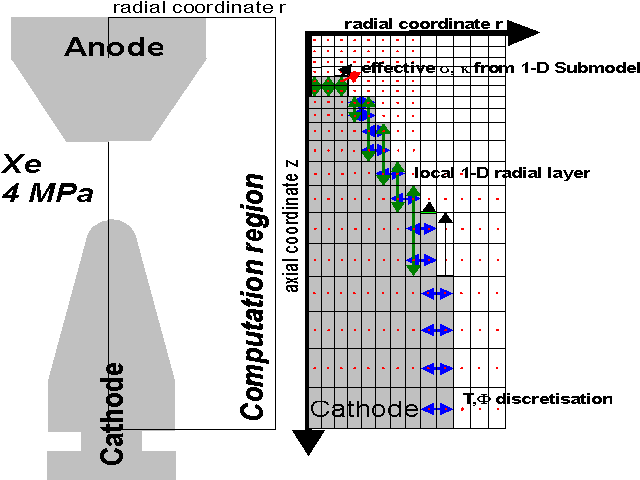
The cathode surface temperatures and electrical current densities have to be computed self-consistently, rather than prescribed. The approach sketched here is an iterative scheme linking the (2-D) electrode and LTE-plasma models by a locally 1-D sub-layer model. The overall computation region is selected as the part of the lamp significantly affected by the discharge details (figure 1).

Fig. 1: Schematic diagram of the computation region (left) and the discretisation details for the boundary layer.
2.1 The arc electrode system
The description of the LTE-arc plasma is composed of fluid flow, heat transport and current continuity balances formulated in cylindrical co-ordinates and solved by finite difference methods [8]. Inside of the electrodes, heat and current transport is computed. Temperature dependent transport coefficients are used [7,12-14].
For the iterative linkage of the plasma and electrode current and heat flow calculations the simple approach of conjugate heat transfer is used. This method implies the description of the locally 1-D boundary layers (anode and cathode sheath) by effective electric and thermal conductivities. These have to be derived from the locally 1-D sub-layer description (transfer function approach).
2.2 Lamp configuration and results
The lamp investigated here and by Hoppstock [7] is a 4 MPa Xenon short arc lamp with 2mm arc length (see figure 1). For a 1:1000 TlI doping, the cathode spot constricts at 8 A.
First results were computed by discarding any sheath model, but adding an additional heat flux at the cathode surface (electron emission cooling, ion heating and thermal radiation loss [10]), a no-sheath transfer-function. The plasma shows a diffuse attachment to the cathode for all currents. At 9A, temperature and flow fields are in good agreement with experimental data. The computed arc voltage is too small by the amount of the cathode sheath drop not included in the model (7V, [7]).
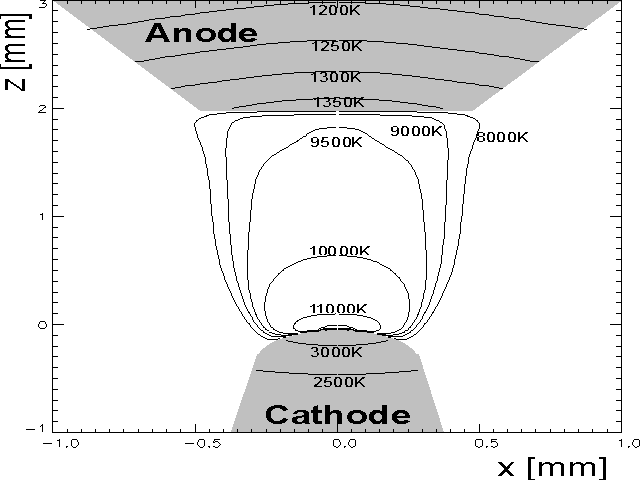
The ambipolar diffusion model of Lowke et.al. [10] is able to produce results for atmospheric argon arcs, but it is not applicable for the plasma regime in the lamps investigated here. A 1-D model for a collision dominated space charge sheath [11] was used for the cathode and gives arc voltages 1-2V below measured (using the no-sheath model for the anode). At 7.5 A, convergence becomes too slow to judge the modelís ability to describe the spot transition. The temperature distribution at 9A agrees with spectroscopical data within the experimental error (see figure 2 and [7]).
3 Conclusions
The integrated electrode-plasma models developed for 0.1 MPa argon arcs can be adapted for high pressure lamp situations, but different 1-D boundary layer models have to be used.
The transition of the cathode operation mode from diffuse to constricted within a small current range can not be predicted by neglecting the cathode sheath. Additionally, further physical effects may play a role for this phenomenon, e.g.
4 Acknowledgements
Financial support by the BMBF under the "Forscherverbund Lampenkatoden" (Contract No. 13N7105) is gratefully acknowledged.
5 References